Sunday 14 October 2012
Wednesday 10 October 2012
The Art Of Percentage .
THE ART OF PERCENTAGE
7 5/100 = 705 % 13 67/100 = 1367 %
7 = 700 % 13 = 1300 %
5/100 = 5 % 67/100 = 67 %
700 % + 5 % = 705 % 1300 % + 67 % =1367%
---------------------------------------------------------------------------------
3 3/4 = 375 % 5 6/10 = 560 %
3 = 300 % 5 = 500 %
3/4 = 75 % ( 25 % X 3 ) 6/10 X 10 = 60 %
300 % + 75 % = 375 % 500 % + 60 % = 560%
---------------------------------------------------------------------------------
28.75 = 2875 %
28 75/100 = 2875 %
Monday 8 October 2012
Visit our School Blog
Our school has a blog for pupils or visitors to explore .
Click this link here to go to the blog
SCHOOL BLOG
Click this link here to go to the blog
SCHOOL BLOG
Sunday 7 October 2012
About Us
* BLOG TITLE
= MATHEMATICS ROCKS !
* GROUP NAME
= PRO-MATH BLOGGERS .
= PRO-MATH BLOGGERS .
* MEMBERS OF THE GROUP
= Yusuf Budiawan , Faris Amran , Fikri Suhail Amer .
* CLASS
* CLASS
= 6 BAIDURI
* AGE
= 12 YEARS OLD ( ALL OF THE MEMBERS )
* TEACHER IN CHARGE
= TC . RUTH LING
* BLOG ' URL '
= matheisfun.blogspot.com
* TEACHER IN CHARGE
= TC . RUTH LING
* BLOG ' URL '
= matheisfun.blogspot.com
Percentage
Percentages (%)
When you say "Percent" you are really saying "per 100"
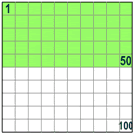 | So 50% means 50 per 100 (50% of this box is green) | And 25% means 25 per 100 (25% of this box is green) | 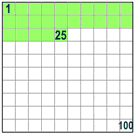 | |
Examples:
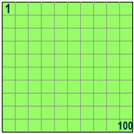 |
100% means all.
Example:
100% of 80 is 100/100 × 80 = 80
| |
 |
50% means half.
Example:
50% of 80 is 50/100 × 80 = 40
| |
 |
5% means 5/100ths.
Example:
5% of 80 is 5/100 × 80 = 4
|
Using Percent
Because "Percent" means "per 100" you should think "this should always be divided by 100"
So 75% really means 75/100
And 100% is 100/100, or exactly 1 (100% of any number is just the number, unchanged)
And 200% is 200/100, or exactly 2 (200% of any number is twice the number)
Use the slider on the left and try some different numbers (example, what is 40% of 80?)
|
A Percent can also be expressed as a Decimal or a Fraction
 |
|
Read more about this at Decimals, Fractions and Percentages.
Some Worked Examples
Example: Calculate 25% of 80
25% = 25/100
(25/100) × 80 = 20
So 25% of 80 is 20
Example: 15% of 200 apples were bad. How many apples were bad?
15% = 15/100
(15/100) × 200 = 15 × 2 = 30 apples
30 apples were bad
Example: if only 10 of the 200 apples were bad, what percent is that?
As a fraction, 10/200 = 0.05
As a percentage it is: (10/200) x 100 = 5%
5% of those apples were bad
Example: A Skateboard is reduced 25% in price in a sale. The old price was $120. Find the new price
First, find 25% of $120:
25% = 25/100
(25/100) × $120 = $30
25% of $120 is $30
So the reduction is $30
Take the reduction from the original price
$120 - $30 = $90
The Price of the Skateboard in the sale is $90
The Word
"Percent" comes from the latin Per Centum. The latin word Centum means 100, for example a Century is 100 years.
Percent vs Percentage
My Dictionary says "Percentage" is the "result obtained by multiplying a quantity by a percent". So 10 percent of 50 apples is 5 apples: the 5 apples is the percentage.
But in practice people use both words the same way.
Tuesday 25 September 2012
Numbers
In mathematics, you'll see many references about numbers. Numbers can be
classified into groups and intially it may seem somewhat perplexing but
as you work with numbers throughout your education in math, they will
soon become second nature to you. You'll hear a variety of terms being
thrown at you and you'll soon be using those terms with great
familiarity yourself. You will also soon discover that some numbers will
belong to more than one group. For instance, a prime number is also an integer and a whole number. Here is a breakdown of how we classify numbers:
Rational Numbers
Rational numbers have integers AND fractions AND decimals. Now you can see that numbers can belong to more than one classification group. Rational numbers can also have repeating decimals which you will see be written like this: 0.54444444... which simply means it repeats forever, sometimes you will see a line drawn over the decimal place which means it repeats forever, instead of having a ...., the final number will have a line drawn above it.
Irrational Numbers
Irrational numbers don't include integers OR fractions. However, irrational numbers can have a decimal value that continues forever WITHOUT a pattern, unlike the example above. An example of a well known irrational number is pi which as we all know is 3.14 but if we look deeper at it, it is actually 3.14159265358979323846264338327950288419.....and this goes on for somewhere around 5 trillion digits!
Rational Numbers
Rational numbers have integers AND fractions AND decimals. Now you can see that numbers can belong to more than one classification group. Rational numbers can also have repeating decimals which you will see be written like this: 0.54444444... which simply means it repeats forever, sometimes you will see a line drawn over the decimal place which means it repeats forever, instead of having a ...., the final number will have a line drawn above it.
Irrational Numbers
Irrational numbers don't include integers OR fractions. However, irrational numbers can have a decimal value that continues forever WITHOUT a pattern, unlike the example above. An example of a well known irrational number is pi which as we all know is 3.14 but if we look deeper at it, it is actually 3.14159265358979323846264338327950288419.....and this goes on for somewhere around 5 trillion digits!
Sunday 23 September 2012
Subscribe to:
Posts (Atom)
