How to solve percentage problems

The Art Of Percentage .

THE ART OF PERCENTAGE

7 5/100 = 705 %                                                          13 67/100 = 1367 %

7 = 700 %                                                    13 = 1300 % 

5/100 = 5 %                                                 67/100 = 67 %

700 % + 5 % = 705 %                                 1300 % + 67 % =1367%

---------------------------------------------------------------------------------

3 3/4 = 375 %                                                 5 6/10 = 560 % 

3 = 300 %                                                    5 = 500 %

3/4 = 75 % ( 25 % X 3 )                              6/10 X 10 = 60 %

300 % + 75 % = 375 %                               500 % + 60 % = 560%

---------------------------------------------------------------------------------

28.75 = 2875 %

28 75/100 = 2875 %

Visit our School Blog

Our school has a blog for pupils or visitors to explore .

Click this link here to go to the blog

SCHOOL BLOG

Or , if you want to our school website , you can click this link .

SCHOOL WEBSITE

About Us

* BLOG  TITLE 

= MATHEMATICS ROCKS !

* GROUP NAME

= PRO-MATH BLOGGERS . 

* MEMBERS OF THE GROUP 

= Yusuf Budiawan , Faris Amran , Fikri Suhail Amer . 

* CLASS 

= 6 BAIDURI 

* AGE 

= 12 YEARS OLD ( ALL OF THE MEMBERS ) 


* TEACHER IN CHARGE

= TC . RUTH LING 


* BLOG ' URL ' 


= matheisfun.blogspot.com
 

Percentage

Percentages (%)

When you say "Percent" you are really saying "per 100"

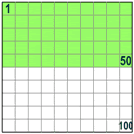	So 50% means 50 per 100 (50% of this box is green)		And 25% means 25 per 100 (25% of this box is green)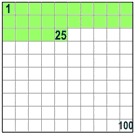

Examples:

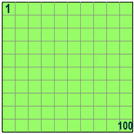		100% means all. Example: 100% of 80 is 100/100 × 80 = 80
		50% means half. Example: 50% of 80 is 50/100 × 80 = 40
		5% means 5/100ths. Example: 5% of 80 is 5/100 × 80 = 4

Using Percent Because "Percent" means "per 100" you should think "this should always be divided by 100" So 75% really means 75/100 And 100% is 100/100, or exactly 1 (100% of any number is just the number, unchanged) And 200% is 200/100, or exactly 2 (200% of any number is twice the number) Use the slider on the left and try some different numbers (example, what is 40% of 80?)

A Percent can also be expressed as a Decimal or a Fraction

A Half can be written...       As a percentage: 50% As a decimal: 0.5 As a fraction: 1/2

Read more about this at Decimals, Fractions and Percentages.

Some Worked Examples

Example: Calculate 25% of 80

25% = ²⁵/₁₀₀

(²⁵/₁₀₀) × 80 = 20

So 25% of 80 is 20

Example: 15% of 200 apples were bad. How many apples were bad?

15% = ¹⁵/₁₀₀

(¹⁵/₁₀₀) × 200 = 15 × 2 = 30 apples

30 apples were bad

Example: if only 10 of the 200 apples were bad, what percent is that?

As a fraction, 10/200 = 0.05

As a percentage it is: (10/200) x 100 = 5%

5% of those apples were bad

Example: A Skateboard is reduced 25% in price in a sale. The old price was $120. Find the new price

First, find 25% of $120:

25% = ²⁵/₁₀₀

(²⁵/₁₀₀) × $120 = $30

25% of $120 is $30

So the reduction is $30

Take the reduction from the original price

$120 - $30 = $90

The Price of the Skateboard in the sale is $90

The Word

"Percent" comes from the latin Per Centum. The latin word Centum means 100, for example a Century is 100 years.

Percent vs Percentage

My Dictionary says "Percentage" is the "result obtained by multiplying a quantity by a percent". So 10 percent of 50 apples is 5 apples: the 5 apples is the percentage.

But in practice people use both words the same way.

Question 1 Question 2 Question 3 Question 4 Question 5 Question 6 Question 7 Question 8 Question 9 Question 10  

Numbers

In mathematics, you'll see many references about numbers. Numbers can be classified into groups and intially it may seem somewhat perplexing but as you work with numbers throughout your education in math, they will soon become second nature to you. You'll hear a variety of terms being thrown at you and you'll soon be using those terms with great familiarity yourself. You will also soon discover that some numbers will belong to more than one group. For instance, a prime number is also an integer and a whole number. Here is a breakdown of how we classify numbers:   
Rational Numbers
Rational numbers have integers AND fractions AND decimals. Now you can see that numbers can belong to more than one classification group. Rational numbers can also have repeating decimals which you will see be written like this: 0.54444444... which simply means it repeats forever, sometimes you will see a line drawn over the decimal place which means it repeats forever, instead of having a ...., the final number will have a line drawn above it.                    
Irrational Numbers
Irrational numbers don't include integers OR fractions. However, irrational numbers can have a decimal value that continues forever WITHOUT a pattern, unlike the example above. An example of a well known irrational number is pi which as we all know is 3.14 but if we look deeper at it, it is actually 3.14159265358979323846264338327950288419.....and this goes on for somewhere around 5 trillion digits!   

Math blog .

MATHEMATICS IS FUN !